在當今量子計算領域,雖然量子計算機被寄予厚望能夠超越經典計算機的計算能力,但現實面臨諸多挑戰。當前技術的限制使得構建具備量子糾錯功能的通用數字量子計算機仍難以實現,主要源于現有技術的嘈雜性與不完善性。受經典計算進化歷程的啟發,一種全新的計算范式 —— 數字模擬量子計算(DAQC)應運而生。這種范式巧妙地將數字量子計算的靈活性與模擬量子模擬的魯棒性相融合,為量子計算的發展開辟了新的路徑。
微云全息在這一新興范式下積極探索,提出了一種高效的數字模擬量子算法專門用于計算量子傅里葉變換。量子傅里葉變換作為一種在多種相關量子算法中廣泛應用的子程序,其計算效率與精度的提升對于整個量子算法體系的發展具有極為關鍵的意義。
在對噪聲模型進行合理假設的基礎上,微云全息深入研究發現,隨著所涉及量子比特數量的逐步增加,運用該數字模擬量子算法進行量子傅里葉變換的保真度能夠得到顯著提高。這一成果的達成,得益于微云全息對算法編寫的深入鉆研以及對數字模擬量子計算范式的有效運用。
微云全息在研究過程中,選取齊次全對全(ATA)兩體 Ising 模型作為 DAQC 實現的基礎資源,并進一步將其哈密頓量表示為非齊次 ATA 兩體 Ising 模型。通過這種方式,為算法的有效實施構建了堅實的理論框架。
為了驗證算法的有效性與優越性,微云全息進行了大量的數值模擬實驗。針對 3、5、6 和 7 量子位器件的情況展開深入研究,在模擬過程中,充分考慮并引入了相互作用中的合理噪聲模型,力求使實驗環境貼近真實的量子計算場景。此外,微云全息還運用純數字方法和 DAQC 方法對特定狀態族進行了全面測試。測試結果清晰地表明,理想變換與 DAQC 實現的變換之間的保真度隨著量子比特數的上升,在質量上明顯優于純數字實現所提供的保真度。
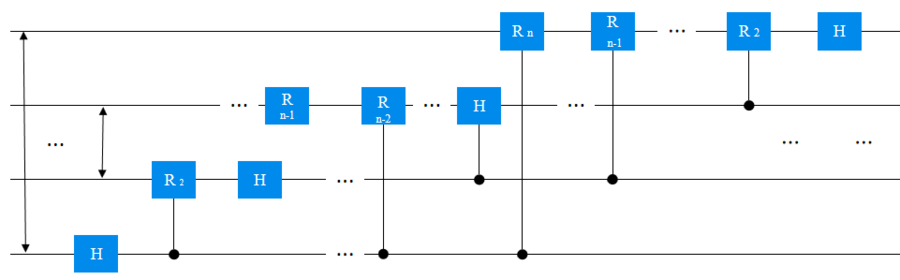
盡管數字模擬量子計算這一新興模式自身也存在一定的噪聲源,但它成功地消除了由糾纏雙量子比特門所產生的誤差。這一關鍵特性使得微云全息能夠在嘈雜的中等規模量子(NISQ)時代,突破現有技術困境,成功實現相關的量子算法。這一成果充分彰顯了在當前 NISQ 時代背景下,結合數字和模擬量子計算的混合協議極有可能成為實現量子計算領域 “有用量子霸權” 的一種極為明智且有效的方法。
微云全息將繼續深入探索數字模擬量子計算范式,不斷優化相關算法,致力于推動量子計算技術在實際應用場景中的落地與發展,為全球量子計算技術的進步貢獻自身的力量,也為與各界合作伙伴攜手共創量子計算的輝煌未來奠定堅實的基礎。
